What is the effect of a treatment on health outcomes? The real question is: can you be more specific?
Researchers may measure the treatment effect a variety of ways. Sensible research questions include:
- What is the average effect of the treatment across all individuals?
- What is the average treatment effect only among those who received treatment?
- What is the difference in the treatment effect between those who are more likely to receive treatment compare to others?
- What is the difference in the treatment effect between those who are marginally more likely to receive treatment compare to others?
Question 2 differs from 1 when the people who receive treatment are more (or less) likely to benefit from it. For instance, one could consider a case where patients either receive surgery or watchful waiting. If patients who receive surgery are exactly those who are more likely to benefit, one many be interested in answering question 2 rather than question 1, since including the people who don’t get surgery (since they don’t benefit from it) may dilute the measured effect of interest.
Questions 3 and 4 are similar, except that question 3 examines the difference in outcomes for individuals with different average treatment probability whereas question 4 examines the derivative. More specifically, question 4 aims to answer what the is the average effect for people who are just indifferent between receiving treatment or not at a given value of the instrument.
One can answer these four questions using the following four parameters:
- Average Treatment Effect (ATE)
- Expected effect of treatment on the treated (TT)
- Local Average Treatment Effect (LATE)
- Marginal Treatment Effect (MTE) or Local Instrumental Variables (LIV)
Each of these is defined below from Heckman and Vytlacil (1999).
where Δ is the change in outcomes, X is the covariates of interest.
![]()
In this equation, and D is an indicator for whether the individual received a treatment. One can also incorporate a propensity score P(Z) based on a set of instruments Z.
For a given propensity score, one can also calculate the treatment effect on the treated as:

When moving to examining how a change in the probability of treatment effects outcomes, one must calculate either LATE or LIV.
LATE gives the average treatment effect for those who would have been effected by the instrument. Consider the case of examining the impact of military service on earnings where draft lottery status is an instrument for military service. This IV approach identify the effect of military service on individuals who would always join the military or those who would never join the military. (it is assumed that there are no “defiers” that join the military when they are not drafted and do not join the military when they are drafted). Thus, LATE only identifies the effect of military service on “compliers”, those would would join the army if drafted, but would not join if not drafted. The IV strategy only identifies ATE if all individuals are compliers, in which case LATE and ATE are equivalent.
LIV is the limit form of the LATE parameter and is defined as follows:
As Heckman, Urzua and Vytlacil explain, to compute this value, the probability of being treated (conditional on covariates X) must fall between 0 and 1 (i.e., 0<P(D=1|X) <1). In other words, for each set of individuals with covariates X, there must exist both a treatment and comparison group.
Heckman and Vytlacil (1999) show that different treatment effect parameters can be seen as averaged versions of the LIV parameter that differ according to how they weight the LIV parameter.
ATE weights all LIV parameters equally. LATE gives equal weight to the LIV parameters within a given interval. TT gives a large weight to those LIV parameters corresponding to the treatment effect for individuals who are the most inclined to participate in the program.
For more information on local instrumental variables (LIV) see my previous post.
Source:
- Basu A, Heckman JJ, Navarro-Lozano S, Urzua S. Use of instrumental variables in the presence of heterogeneity and self-selection: an application to treatments of breast cancer patients. Health Econ. 2007 Nov;16(11):1133-57.
- Heckman, J.J. and E.J. Vytlacil, Local instrumental variables and latent variable models for identifying and bounding treatment effects. Proc Natl Acad Sci U S A, 1999. 96(8): p. 4730-4.
- Heckman, J., J., S. Urzua, and E. Vytlacil, Understanding Instrumental Variables in Models with Essential Heterogeneity. The Review of Economics and Statistics, 2006. 88(3): p. 389-432.
- Guido W. Imbens and Joshua D. Angrist. Identification and Estimation of Local Average Treatment Effects. Econometrica , Vol. 62, No. 2 (Mar., 1994), pp. 467-475.
- Joshua D. Angrist. Lifetime Earnings and the Vietnam Era Draft Lottery: Evidence from Social Security Administrative Records. The American Economic Review , Vol. 80, No. 3 (Jun., 1990), pp. 313-336
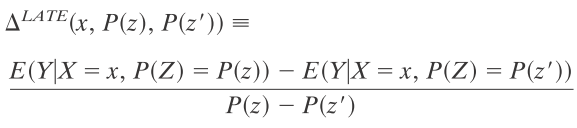
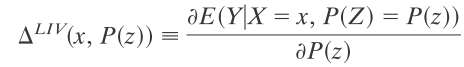
We have noticed that your article is related to Life Sciences matters and have been mentioned on Biowebspin, the Bio Dashboard for the largest netwok in Biotech, Pharma & Medtech. Here is the link :
http://www.biowebspin.com/members/nicolasr/activity/121969/
You can also post your abstract of your articles on Biowebspin Public Place (http://www.biowebspin.com/activity/) and be seen by thousands of Life Sciences visitors all across the globe.
Best Regards,
The Biowebspin’s team.