What is the standard error of a predicted value? Most people know that the standard error of the mean of a dependent variable is σ(Z_bar)= σ(Z_bar) / √N. As Dowd, Greene and Norton (2013) explain, however, the standard error for the predicted value of a linear regression is much more complicated:
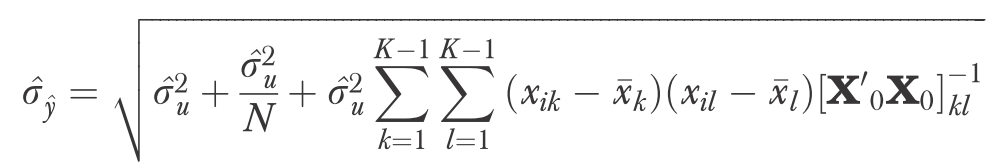
The estimated standard error of the predicted values y_hat combines four factors:
- The deviation of y_hati from the sample regression line due to unobserved factors ui
- The deviation of the sample regression line itself from the true regression line
- The sampling variation of xi
- The distance of x from the sample mean, x_bari.
Other complications occur when computing standard errors for the partial effects when the relationship between the dependent and independent variables are non-linear (e.g., logit, squared regression terms).
The authors evaluate three methods for computing standard errors in these situations.
- The Delta Method. The delta method is the most common method of calculating the standard errors of partial effects in most software packages. The delta method uses afirst-order Taylor series expansion.
- Krinsky and Robb (K-R) method is based on the assumption that the estimators of the modelparameters are consistent and have an asymptotically normal multivariate distribution. The K–R method draws multiple vectors of β coefficients from the multivariate normal distribution that has a mean vector equal to the original estimated coefficient vector and the same estimated variance-covariance matrix. Each new vector of coefficients, b s , is used to compute a new value of the function of interest.
- The bootstrap approach also applies many “draws” of coefficient vectors β , to the sample observations, but variation in the coefficient vectors is obtained by re-estimating the model many times on different data samples. Each new data sample is obtained by drawing N observations with replacement from the original sample of data
The authors find little difference in using any of these methods to compute standard errors and claim that use of the Delta Method, K-R method and bootstrap approach should be made mostly out of convenience.
Source:
- Dowd, B. E., Greene, W. H. and Norton, E. C. (2013), Computation of Standard Errors. Health Services Research. doi: 10.1111/1475-6773.12122
So this post was just a math review from calc and diff eq? I feel like you could just say that something is more complicated than you realize and then just post a math equation with partials and vectors and blow peoples’ mind.
Granted, I’m not saying this isn’t tricky, but I do think that working with SE’s should require you to understand the factors taken into account.